Faster processor communications to better understand fluid turbulences

Published on 05/09/2023
Pierre Balty is a PhD. student with Prof. P. Chatelain at the Institute of Mechanics, Materials, and Civil Engineering at the UCLouvain. The main focus of their research group is the theoretical investigation of turbulence in fluids, also known as computational fluid dynamics (CFD). This field of study is of great interest to develop wind turbines with better yield, planes with low consumption, or aerodynamic cars. In such devices, small perturbations can dramatically influence the fluid's behavior at large scales. Therefore, it is important to have efficient numerical tools that accurately perform CFD computations of large domains that resolve the most minor details in a reasonable amount of time.
Pierre Balty: “One of the Vortex and Turbulence Research Group's interests lies in understanding and exploring fluid phenomena at an unprecedented level of accuracy. The latter often implies many different scales, requiring a substantial number of unknowns and, hence very large computational resources."
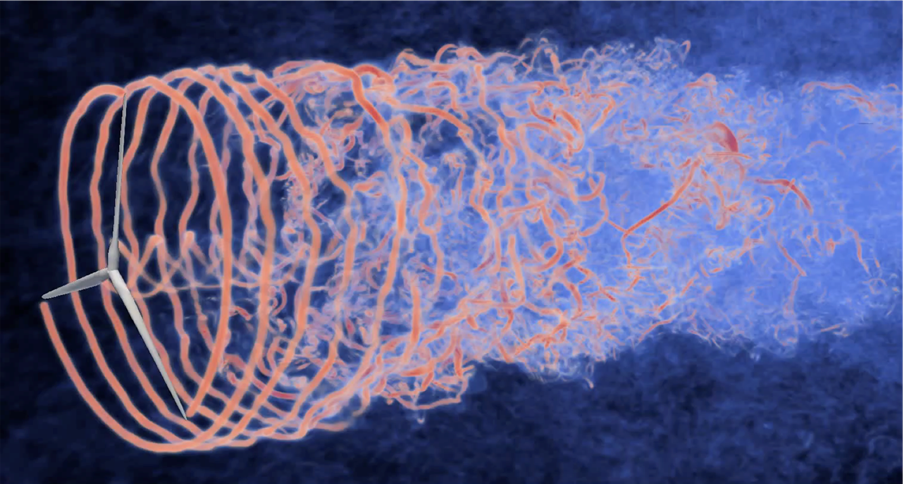
Volume rendering of vorticity magnitude behind a wind turbine.
Chatelain, P., Backaert, S., Winckelmans, G. et al. Large Eddy Simulation of Wind Turbine Wakes. Flow Turbulence Combust 91, 587–605 (2013).
https://doi.org/10.1007/s10494-013-9474-8
High-performance computing, a necessity for CFD
Pierre Balty: “HPC is a key element in our research fields. Most of our simulations cannot be done on a personal computer in terms of memory or time-to-solution. For example, some simulations take 16 hours to run on an HPC architecture, whereas it would have taken six months on a personal computer."
However, using supercomputers is not straightforward, and appropriate methods are needed to take advantage of their complex structures. In particular, the algorithms must be optimized to perform time-efficient calculations. The most time-consuming part of CFD simulations is the 3D unbounded Poisson equation. The Poisson equation is well-known in physics and mathematics. For CFD simulations, Poisson’s equation is required to impose the fluid incompressibility, which is, fortunately, a good approximation for the relevant applications. The project of Pierre Balty, supervised by Thomas Gillis, is focused on developing an integrated software combining versatility, performance, scalability, and portability to solve this Poisson equation.
A communication bottleneck
The main problem is that solving the Poisson equation scales poorly when using many processors on a supercomputer.
Pierre Balty: “The Poisson problem is an elliptic problem, where each point in the domain influences all the other points.”
In other words, the behavior of the fluid at one point in space influences the behavior of the fluid at any other point. This has critical consequences for HPC calculation: solving such problems requires “all-to-all” communications, which means that the processing units need to communicate all together. These communications bound the total calculation time.
To solve the Poisson equation, they proposed an approach based on the Fast Fourier transform (FFT), a well-known method to speed up calculations when dealing with uniform and regular cartesian grids. Here, FFTs in 3 dimensions are computed using a series of 1D FFTs. But this method requires the data to be aligned and continuous in the memory for each 1D FFT, which thus requires communications to rearrange the data for each 1D FFT, and these communications become the algorithm bottleneck.
Pierre Balty: “We proposed different implementations where the overall objective was to reduce the strong synchronisation of the CPUs and improve the parallelisation without impacting the flexibility and versatility of the solver.”
One of the indicators of performance for their implementation is the scalability. Scalability is crucial for users when using HPC systems. For exascale architecture, where resources are tremendous, one of the key factors is the strong scalability, i.e., the ability of the software to decrease the time-to-solution proportionally to the increase of the number of processes.
Pierre Balty: ”If the user doubles the number of processors, it divides the time-to-solution not by two but slightly less, by 2 x η where η, the strong scalability is between 0 and 1. The higher the η, the larger the time gain. In our case, the strong efficiency is remarkable for an “all-to-all” problem.”
Beyond Fluid dynamics
However, the impact of their works goes well beyond computational fluid dynamics. The Poisson equation is ubiquitous in computational physics as it concerns problems ranging from particle physics to electromagnetism.
Pierre Balty: "Thanks to the enormous computational resources they provide, HPC is a keystone in such fields. Currently, the focus is on porting the existing frameworks on GPUs to benefit from the full computational power those supercomputers provide. For low arithmetic intensity problems such as the Poisson problem, the high bandwidth provided by the recent HPC architecture promises considerably reduced times-to-solution."
Related links
GitHub repository of their program FLUPS: https://github.com/vortexlab-uclouvain/flups
Article 1: https://ieeexplore.ieee.org/document/10064099
Article 2: https://epubs.siam.org/doi/10.1137/19M1303848
Webpage of Philippe Chatelain's research group: https://uclouvain.be/en/research-institutes/immc/turbulence-and-vortical-flows.html

Pierre Balty received the master’s degree from UCLouvain, in 2019 and is currently working toward the PhD degree under the supervision of Prof. Philippe Chatelain within the Institute for Mechanics, Material, and Civil engineering, UCLouvain. His research focuses on hybrid Eulerian-Lagrangian numerical methods, their deployment on distributed systems, and their applications to wind energy. To pursue his research, Pierre collaborate with international research group from the Massachusetts