User Story: Transforming Burn Care with Mathematical Modelling and Supercomputing
Published on 22/02/2024
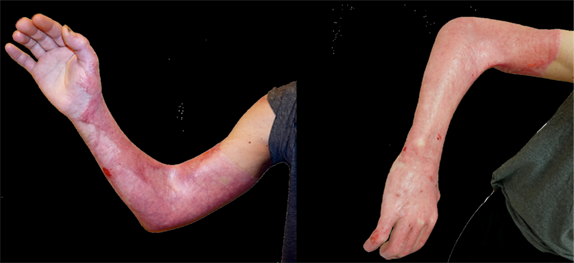
About 120,000 individuals in Belgium endure severe burn injuries annually, whereas about 10,000 individuals need hospitalisation; the aftermath extends far beyond visible scars. The recovery process also introduces skin contractions. These contractions, in turn, can result in mobility problems for the patient, which can even lead to disability. Picture a patient struggling to extend an arm, hampered by skin rigidity, or one unable to lift his head due to the constriction following a neck burn. These limitations in movement have a profound impact on patients' daily activities and lives.
Mathematical modelling, a powerful tool
Therefore, doctors aim for treatments that minimise skin contraction when treating burn injuries.
Mathematical modelling emerges as a powerful tool, offering a virtual canvas to simulate the complex dynamics of human skin contraction. Fred Vermolen, Professor in Computational Mathematics at Hasselt University, explores the intersection of mathematical modelling and supercomputing, introducing a new era in burn injury treatments.
Fred Vermolen (UHasselt): “One of the first challenges is understanding what happens in the skin after a burn injury. Conversations with doctors, surgeons and medical biologists give me profound, valuable insights to do this. The next challenge is translating post-burn skin biology into mathematical equations.”
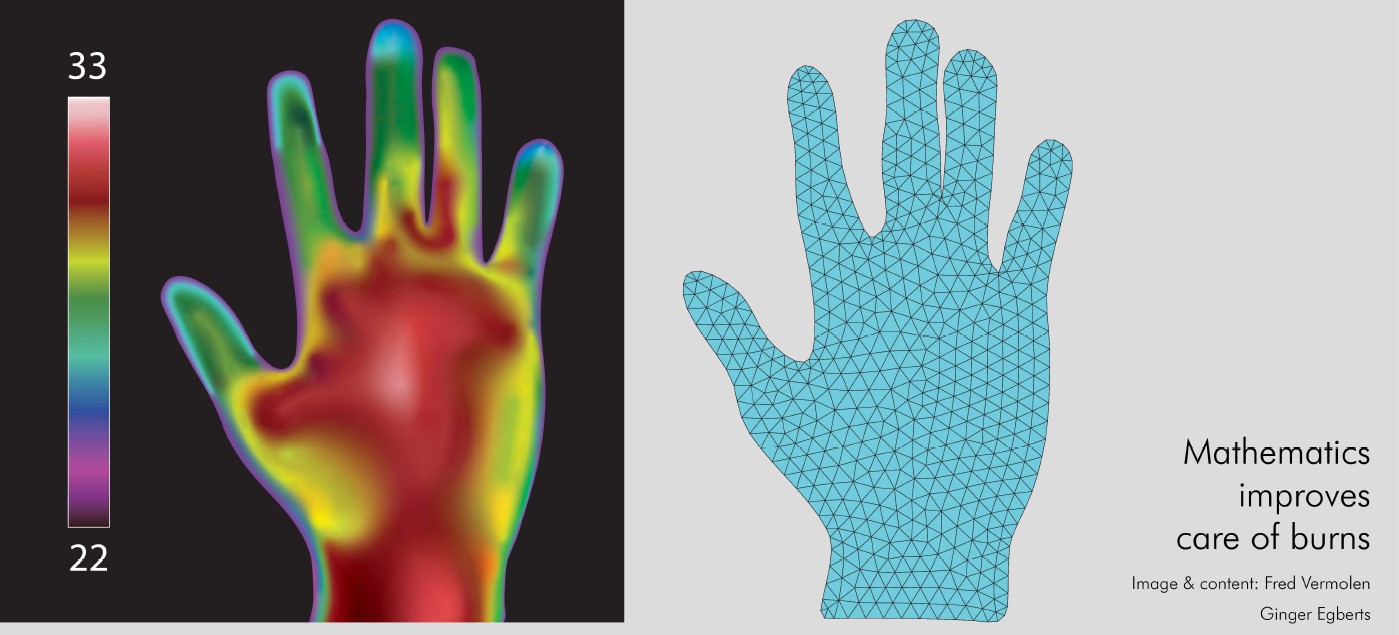
The mathematical framework is based on a continuum formalism that is applicable to the scale of tissues, which fall in the range of centimetres to decimetres. We model cells in terms of their densities [1], which are solutions to conservation laws that are formulated by partial differential equations (PDEs [2]). Because these PDEs are too complex to solve exactly, we are devising strategies to approximate the solution.
Dealing with uncertainty
These PDEs contain many input parameters that are patient-specific. The same burn injury on your skin and an older person's skin can behave differently since age influences the stiffness of the skin. Age, pigmentation, gender, and other factors affect the evolution of a burn injury over time in different patients.
Parameters are sometimes also poorly documented. If a patient with a severe burn injury is hospitalised, the patient may be unconscious, leading doctors to prioritise immediate life-saving measures over meticulous measurement of the wound characteristics. The primary focus is on curing the patient, with little emphasis on detailed wound assessment during these critical moments. Consequently, there is a delay in gathering comprehensive data on wound geometries and sizes, introducing potential errors and inaccuracies. These factors cause uncertainties that impact both post-burn dermal evolution [3] and, hence, the treatment to be chosen. The model should take this form of uncertainty into account as well.
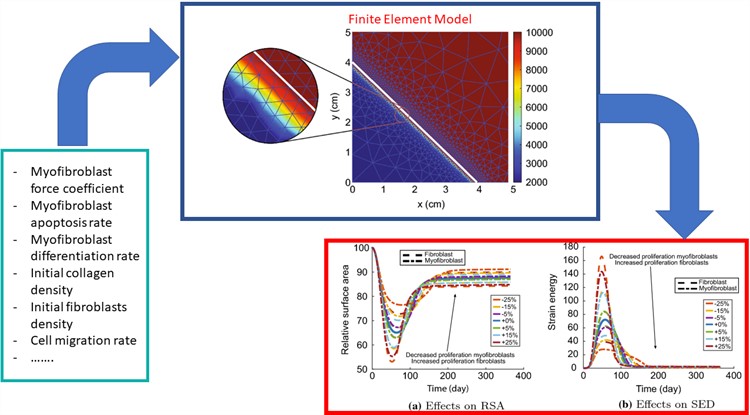
Figure courtesy of Ginger Egberts.
Fred Vermolen (UHasselt): “To deal with these uncertainties, we use the uncertainty quantification method. We estimate the likelihood of different outcomes, such as how much the skin contracts or the overall amount of strain energy (a measure of discomfort experienced by the patient). We run the model many times with different input values sampled from statistical distributions.”
The process involves solving a set of complicated equations using various techniques like finite elements, time integration, and mesh detection. The researchers also use a Monte Carlo-like approach, a method for making statistical estimates through random sampling. This helps them deal with the uncertainties, but it requires a lot of computational power [4].
Training of a neural network
Mathematical modelling gives insight but can also be used to estimate the chances of successful treatment through (clever) multiple realisations of the simulation framework. Since this step is expensive from a computational point of view, neural networks are used to speed up the simulations so that the mathematical framework can be used in clinical practice. For this purpose, training the network and generating data is necessary.
Fred Vermolen (UHasselt): “We used the Tier-2 Vlaams Supercomputer Center (VSC) infrastructure to generate the data needed to train the neural network. The computing infrastructure enabled generating data in parallel using multiple computing nodes. It enabled a fast generation of data and fast training of the neural network. Eventually, a reliable and fast neural network that can reproduce lengthy finite element simulations was obtained. Thanks to using a neural network, simulation times are much shorter.”
In Silico Simulations: a human and accurate alternative to animal testing in research
Prof. Vermolen's research is also partially funded by Stichting Proefdiervrij, a Dutch foundation committed to making the use of laboratory animals in scientific research unnecessary.
Fred Vermolen (UHasselt): "Mathematical modelling can replace animal testing by developing a 'virtual patient’, thus eliminating the need for such experiments on animals. The ethical concerns are significant; for example, inflicting burns on animals to study skin behaviour is not only cruel but also scientifically limited. Animals, though used as models for humans, often do not accurately represent human conditions due to differences in the skin. Hence, virtual models or in silico simulations offer a more ethical and accurate approach."
Future research
Fred Vermolen (UHasselt): “We are extending our models also to more curved geometries (for instance, in the shoulder or the arm). More incorporation of the curvature of the human body is also better for big burns. In the future, our simulations can also be used to see the impact of certain therapies on the progression and evolution of skin. Then, you can think of trying to optimise the therapy, for instance.”
Another possibility for future research is to create the potential for doctors to take a picture of a wound and insert that wound geometry into the computation framework, then calculate the probabilities that this wound will be problematic in terms of conjunction and extreme scaring. This may lead the way to more patient-specific healthcare.
Fred Vermolen (UHasselt): “Ultimately, my dream is to create a digital twin that mirrors not only individual patient anatomy and injury patterns but also revolutionises personalised treatment strategies in burn care, transforming patient outcomes and recovery.”
Experience with VSC: Smooth transition into effective use
Fred Vermolen (UHasselt): “My experience with the VSC team has been commendable. Initially, there was a learning curve, as with any new tool, but the support and responsiveness of the VSC team were very good. They provided valuable guidance, ensuring a smooth transition into effective use. The positive environment fostered by the team enabled us to achieve our objectives, particularly in conducting simulations on the finite element model and other numerical models.”
VSC as the optimal path for computational efficiency
Fred Vermolen (UHasselt): "Every Flemish researcher is entitled to access the robust infrastructure of Vlaams Supercomputer Center. It's a game-changer for those requiring extensive parallel simulations, especially in projects dealing with uncertainty. By utilising VSC Tier-2 infrastructure, researchers can easily access computing power, focusing on their core work. In a nutshell, VSC is a great partner to obtain computational efficiency and practicality in intensive research.
[1] The density of cells is a dynamic parameter: the number of cells per unit volume of skin will change with location and over time (the wound is also a dynamical entity because it can be healing or developing into a scar). This means the partial differential equations can be seen as a conservation of entities from a physical point of view.
[2] Source: https://sinews.siam.org/Details-Page/can-mathematics-help-patients-with-burn-injuries
[3] Source: https://sinews.siam.org/Details-Page/can-mathematics-help-patients-with-burn-injuries
[4] Source: https://sinews.siam.org/Details-Page/can-mathematics-help-patients-with-burn-injuries
Relevant links

Fred Vermolen is full Professor in Computational Mathematics at the University of Hasselt, Belgium. Prof. Vermolen's research is in the field of free boundary problems (Stefan problems during his PhD work), partial differential equations, numerical approaches and uncertainty quantification, with applications in medicine and porous media. Prof. Vermolen was an assistant and associate professor at the Delft University of Technology in the Netherlands. He has done short sabbaticals in the UK and Sweden and a long sabbatical in Germany